
6.缓解率曲线描绘以横轴为随访天数(n),纵轴为累计缓解率(np0),将两疗法的演算结果各点的坐标准确标出,然后将各点向右连成与横轴平行的阶梯形,得出两组缓解曲线如图23-1。可以看出乙疗法累计缓解率水平始终在甲法之上。
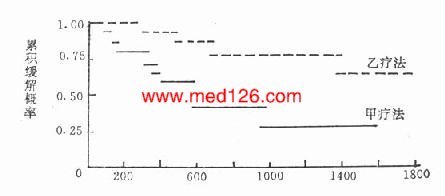
图23-1 甲、乙疗法累计缓解率的比较
二、两疗法差异的统计学意义分析
如果要分析两疗法差异有无统计学意义,可用时序检验法(log rank test)。假定两组疗法效果相同,求各时点预期复发数,再进一步作x2检验。演算如表23-5。医.学 全,在.线,提供www.med126.com
表23-5按检验假设算得甲、乙两组的预期复发数(即理论值)和实际数,分别为:
A甲=9,T甲=5.138;A乙=4,T乙=7.817
代入x2检验公式
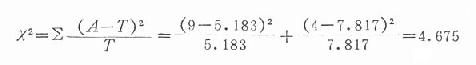
查x2值表,x20.05(1)=3.84,今x2>4.675,P<0.05,表明两法累计缓解率曲线的差别有统计学意义。
表23-5 甲、乙两疗法预期复发数计算表
| 疗法分组(1) | 观察天数(2) | 复发例数 | 期初病例数 | 预期复发数 | |||||
| 甲组(3) | 乙组(4) | 合计(5)=(3)+(4) | 甲组(6) | 乙组(7) | 合计(8)=(6)+(7) | 甲组(9)=(5)(6)/(8) | 乙组(10)=(5)(7)/(8) | ||
| 甲 | 86 | 1 | 1 | 15 | 14 | 29 | 0.517 | 0.483 | |
| 甲 | 141 | 1 | 1 | 14 | 14 | 28 | 0.500 | 0.500 | |
| 甲 | 173 | 1 | 1 | 13 | 14 | 27 | 0.481 | 0.519 | |
| 甲 | 173+ | … | 12 | 14 | 26 | … | … | ||
| 乙 | 296 | 1 | 1 | 11 | 14 | 25 | 0.440 | 0.560 | |
| 甲 | 812 | 1 | 1 | 11 | 13 | 24 | 0.458 | 0.542 | |
| 甲 | 364 | 1 | 1 | 10 | 13 | 23 | 0.435 | 0.565 | |
| 甲 | 401 | 1 | 1 | 9 | 13 | 22 | 0.409 | 0.591 | |
| 甲 | 498+ | … | 8 | 13 | 21 | … | … | ||
| 乙 | 505 | 1 | 1 | 7 | 13 | 20 | 0.350 | 0.650 | |
| 甲
甲 |
570
>570 |
1
>2 1 |
1
> 1 |
7 | 12 | 19 | 0.737 | 1.263 | |
| 乙 | 570+ | … | 5 | 12 | 17 | … | |||
| 乙 | 615+ | … | 5 | 11 | 16 | … | |||
| 乙 | 688 | 1 | 1 | 5 | 10 | 15 | 0.333 | 0.667 | |
| 乙 | 822+ | … | 5 | 9 | 14 | … | … | ||
| 甲 | 836+
> 836+ |
…
… > … |
5
|
8
|
13 | … | … | ||
| 甲 | |||||||||
| 甲 | 950 | 1 | 1 | 3 | 8 | 11 | 0.273 | 0.727 | |
| 乙 | 1190+ | … | 2 | 8 | 10 | … | … | ||
| 乙 | 1205+ | … | 2 | 7 | 9 | … | … | ||
| 乙 | 1375 | 1 | 1 | 2 | 6 | 8 | 0.250 | 0.750 | |
| 乙 | 1408+ | … | 2 | 5 | 7 | … | … | ||
| 甲 | 1446+ | … | 2 | 4 | 6 | … | … | ||
| 乙 | 1493+ | … | 1 | 4 | 5 | … | … | ||
| 甲 | 1540+ | … | 1 | 3 | 4 | … | … | ||
| 乙 | 1570+ | … | 0 | 3 | 3 | … | … | ||
| 乙 | 1645+ | … | 0 | 2 | 2 | … | … | ||
| 乙 | 1726+ | … | 0 | 1 | 1 | … | … | ||
| 总和 | (A)9 | (A)4 | 13 | 15 | 14 | 29 | (T)5.183 | (T)7.817 | |