
(一)OR、ORMH的可信限和ORi的齐性检验
⒈Miettinen法 即是以显著性检验为基础的(test-based)可信限。计算ORMH的100(1-α)%可信限公式

此公式同样可用于计算单个OR(即从一张四格表数据算出的OR)的可信限。这时,上式中用OR代替ORMH,用x2代替X2Mh 。匹配数据的OR也可同样计算。用函数型电子计算器来算,都很简单。
式中的U,可查标准正态差简表(附表5-1),Uα/2可查α/2单侧检验的Uα值。最常用的95%可信限按下式计算(上限记为ORU,或OR,下限记为ORL或OR):

附录5-1 标准正态差简表
|
α(或β) |
单侧检验时Uα(或Uβ*) |
双侧检验时Uα |
|
0.001 |
3.09 |
3.29 |
|
0.005 |
2.58 |
2.81 |
|
0.010 |
2.33 |
2.58 |
|
0.025 |
1.96 |
2.24 |
|
0.05 |
1.64 |
1.96 |
|
0.10 |
1.28 |
1.64 |
|
0.20 |
0.84 |
1.28 |
|
0.30 |
0.52 |
1.04 |
* 双侧检验时Uβ值与单侧检验时相同
计算实例:表4-4的数据,ORMH=5.55,x2MH=76.84,95%可信限: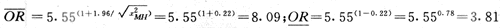
2. Woolf法 即自然对数转换法
(1)首先把OR转移为自然对数,记为lnOR;
(2)按下式求出lnOR的方差,记为Vαr(lnOR):
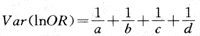
即四格表中每一格数值的倒数之和。倘有某一格的数值为0时,可在每格的数值上各加0.5,再求出它们的倒数之和。
⑶lnOR的100(1-α)%可信限为

如为求95%可信限,上面两式中Uα/2=1.96;
(4)最后各取其反对数(eX),即为OR的可信限。
(5)也可直接用下式算可信限:

以上都是用于计算不分层OR(粗OR)的公式,如为分层的数据也可用Woolf法计算各层lnORi的加权平均数及其可信限;同时可检验各层ORi是否有齐性,即是否没有显著差异,倘有齐性,计算总的OR才有意义。
计算实例:仍用表4-4的数据,用公式(附式5-4)与(附式5-5)分别算出吸烟者与不吸烟者两层中饮酒与食管癌的OR及其对数(lnOR)以及lnOR的方差和方差的倒数(wi权重),结果列表如下:

总的OR用下式计算:

将上表数据代入:

结果与ORMH(5.55)相当接近。再按下式求OR的标准误:
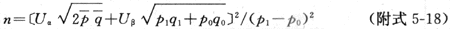 (附式5-9)
(附式5-9)
得Sx(lnOR)=0.2169,于是lnOR的95%可信限lnOR±1.96Sx,代入得2.09,1.24,于是

与ORMH的95%可信限(8.09,3.81)也十分接近。
但是各层的ORi相关悬殊,或即吸烟者与不吸烟者中饮酒与食管癌联系强度差异较大,这种差异是随机变异的机会有多大?可以用下式作x2检验:
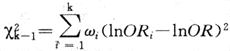 (附式5-10)
(附式5-10)
式中k=层数,自由度=k-1。
代入本例数据,x2=5.06,5.06>x2(1,0.025),p<0.025,各层间的OR差异显著,来自同一总体的可能性很小,所以总的OR不能说明吸烟、饮酒与食管癌的联系,因此是无意义的。
上述x2检验同时可用来检验各因素间是否存在交互作用。本例的结果提示吸烟与饮食这两个因子与食管癌危险度的联系有交互作用。
以上两种方法算得的都是似可信限,但在OR靠近无效值⑴的情况下,特别是在样本较大时,近似法与精确法所得结果十分接近。