分析流行病学有关计算

　　⒊ 匹配数据的OR可信限

　　可用Miettinen法〔以显著性检验为基础的方法，公式（附式5-1)〕，实例见第四章表4-11的数据分析。还可用下述方法：

　　(1)先算方差：

　　(2)OR 的（1－α)％可信限

　　计算实例：仍用表4-11的数据，计算OR的95％可信限。U_α/2＝1.96，OR＝1.71，Var(lnOR)＝(60＋35)/(60×35)＝0.0452，

　　结果与用公式（附式5-1)算得的（1.14，2.57)很接近，而且理论上更恰当。

　　（二)病例对照研究样本含量的估计

　　所谓样本含量估计是指在满足一定条件下的一个粗略估计数；条件变动时估计数会随之发生变化，所以只有相对意义，而不能看作是保证可达到目的的准确数值。

　　样本含量（n)的估计须根据①对照人群的预防暴露率，p0；②暴露与疾病的联系程度，以RR为指标；③假阳性率，即Ⅰ型误差，α；④假阳性率，即Ⅱ型误差，β。

　　1.非匹配设计病例数与对照数相等时每组所需人数

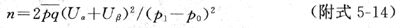
　　式中P₁＝P₀RR/[1＋P₀(RR－1)]，p＝0.5(P₁＋P₀)，q＝1－P₀。U_α与U_β可查附表5-1。有时也可不用公式，通过查表即可得n，例如附表5-2。

附表5-2　病例对照研究样本含量（非匹配，病例组与
对照组人数相等时每组需要人数)

(节录：Schlesselman,1982)

　　例：现拟进行一项病例对照调查，研究吸烟与肺癌的关系。预期吸烟者的相对危险度为10.0，人群吸烟率约0.4。设定α＝0.05（双侧检验)，β＝0.10，查表可见至少需病例与对照各20。样本较小是因RR很大。如用公式（附式5-14)计算，得数也相近，（n≈22)，稍有出入是计算时保留小数位数不同所致。

　　在α＝0.05（双侧检验)时，U_a＝1.96，β＝0.10，U_β＝1.28，于是式（附式5-14)可简化为

　　2. 非匹配设计病例数与对照数不等时

　　设：病例数：对照数1:c，则需要的病例数

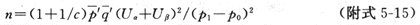
　　式中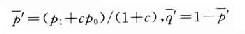，，P1的计算同公式（附5－14)

　　对照数＝cn。

　　3.　1:1匹配（配对)设计　须加估计的不是总例数而是病例与对照暴露情况不同的对子数（即表4-10中的f₁₀与f₀₁)，设为m，则

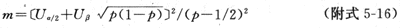
　　式中P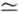RR/(1＋RR)。

　　需要的总对数（f₁₁＋f₁₀＋f₀₁＋f₀₀)设为M，则

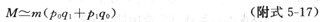
　　式中p₁＝p₀RR/﹝1＋p₀(RR-1)﹞，q₁＝1-p₁，q₀＝1-p₀

　　例：设对照暴露率p₀＝0.3，α＝0.05，β＝0.1，为检出RR＝2需要的

　　m＝[1.96/2＋1.28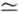186，即共需f₁₀＋f₀₁＝90对，总对数＝186。

上一页  [1] [2] [3] [4] [5] 下一页