
6.生存队列 用生存率分析的方法来描述疾病的预后,可以知道随访过程中各时刻病人死亡或生存的可能性,这就提供了更多的预后信息。分析生存情况,可以先收集一组病人,从病程的同一点(如某种症状或体征的出现、诊断的确立或开始某特定治疗后)开始随访,直至全部病例陆续出现该结果为止。以随访时间为横座标,生存例数为纵座标作图,即可获得阶梯形的生存曲线。图6-8为9例成纤维细胞肉瘤患者开始接受BCNU治疗后的生存曲线。由图可得到任何一天的存活人数。当随访例数相当多时,生存曲线由阶梯型变为光滑的曲线。但多数情况并不如此简单,并非每一个病例都会得到完整的随访,即使经过努力,还会有中途失访的病例。而且,只有等到全部病例都完成随访,才能作出生存率分析。为了有效地应用所得到的随访资料进行生存率分析,一般可使用寿命表方法。
7.寿命表法 生存分析中最常用的方法是寿命表法,它是用以描述人群中死亡和生存情况的一种概括方法,可有效地利用所有资料。它是通过研究一队列人群在其整个生命过程中,当按照一定的年龄别死亡率死亡时,所获得的在特定时间内的累积生存概率。临床常用的寿命表是根据暴露史将人群分组,然后描述各组结局的情况,它说明各组人群任一时点平均发生某一结局的可能性。即求出病人在治疗后活过X年后,再活过下一年的可能性。
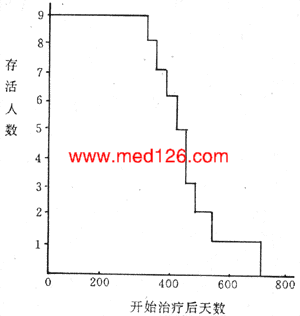
图6-8 BCNU治疗9例成纤维细胞
肉瘤患者的生存情况
如100例手术病人术后第一年内死亡20例;年末存活80例,则术后第一年的生存率P0=80/100=0.80;第二年此80例又有10例死亡,70例生存,则第二年的生存概率为P1=70/80=0.875。求两年累积生存率为70/100。此数值也可由第一年及第二年的生存概率相乘求得:
P2=P0·P1=0.80×0.875=0.70
两种方法计算结果相同。n年之累积生存率为
Px+1=P0·P1·P2…Pn
(式6-8)
在用寿命表法时,任一时点存活的机会,是用活过那一时点之前每段时间的累积存活率估计的。在间隔期内无人死亡,则生存率为1,间隔期内可能有一个或多个病人死亡,这个期间内的生存概率可以用存活数与有死亡危险的人数之比来计算。间隔期内如无一人死亡,则生存概率不变。有些病人早已死亡,已退出研究或在那个时候还没有随访到,因此都不算暴露人数,它们也就不作估计间隔存活情况之用。因此实际上生存概率仅在间隔期内有死亡者才需重新算过。然后以概率论的乘法定律将各年的生存的概率相乘,即得其活过各年的累积生存率。
实例:1965年某市肿瘤医院总结曾在该院作过手术的607例乳腺癌病例随访10年的累积生存率,结果见表6-9。
表6-9 607例乳腺癌术后生存率计算表
| 术后 年数 X (1) |
期内失访人数 Wx (2) |
期内死 亡人数 dx (3) |
期初观察人数 Nx (4) |
订正观 察人数 Nx(5) |
期间死亡概率qx (6) |
期间生存概率Px (7) |
(X+1)年累 积生存率 P(X+1)(8) |
生存率的 标准误 Sp(X+1) (9) |
| 0- | 63 | 59 | 607 | 575.5 | 0.1025 | 0.8975 | 0.8975 | 0.0126 |
| 1- | 71 | 69 | 485 | 449.5 | 0.1535 | 0.8465 | 0.7597 | 0.0186 |
| 2- | 55 | 43 | 345 | 317.5 | 0.1354 | 0.8646 | 0.6568 | 0.0218 |
| 3- | 38 | 30 | 247 | 228.0 | 0.1316 | 0.8684 | 0.5704 | 0.0239 |
| 4- | 31 | 13 | 179 | 163.5 | 0.0795 | 0.9025 | 0.5250 | 0.0252 |
| 5- | 26 | 7 | 135 | 122.0 | 0.0574 | 0.9426 | 0.4949 | 0.0261 |
| 6- | 21 | 14 | 102 | 91.5 | 0.1530 | 0.8470 | 0.4192 | 0.0288 |
| 7- | 11 | 4 | 67 | 61.5 | 0.0650 | 0.9350 | 0.3920 | 0.0301 |
| 8- | 16 | 3 | 52 | 44.5 | 0.0674 | 0.9326 | 0.3656 | 0.0317 |
| 9- | 12 | 0 | 34 | 28.0 | 0.0000 | 1.0000 | 0.3656 | 0.0317 |
医学统计方法。上海科学技术出版社,1978
表6-9的几点说明:
Wx表示X~(X+1)年期间的失访及中断观察人数,由于这些人都随访了X年以上,但不满(X+1)年,所以计算时作1/2人数计算,即算作平均随访了(X+1/2)年。
dx是专指死于乳腺癌的人数,不包括其他死因死亡的人数。
N′x为订正观察人数,含有实际观察人数的意思。
N′x=Nx=1/2wx
例
N′O=NO-WO/2=607-(63÷2)=575.5
qx=dx/ N′x为死亡概率
例 “0-”组死亡概率q0=dx/ N′x=59/575.5=0.1025
px=1-qx为期间生存频率,意指活过X年的可能性,“0-”组生存概率P0=1-0.1025=0.8975
(X+1)年累积生存率P(x+1) 是根据概率的乘法定律将各个期间生存率相乘而得。
(X+1)年的累积生存率P(x+1)=P0·P1·P2……Px
术后活满1年的累积生存率P(0+1)=0.8975
术后活满2年的累积生存率P(1+1)=P0·P1
P(2+1) P3= P0·P1·P2=0.7597×0.8646=0.6568
余类推。生存率的标准误按下式计算:
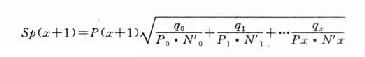 (式6-9)
(式6-9)
例如3年累积生存率的标准误
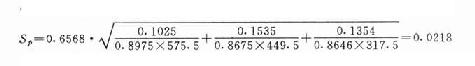
经寿命表法计算出的生存率资料可以制作生存率曲线图。以横座标为时间(年或月),纵座标为生存率(%)作图,将各年生存率按年份点入图中,并用直线连接即可得出生存率曲线。
现以上述607例乳腺癌术后逐年生存资料为例作生存率曲线图(见图6-9)。
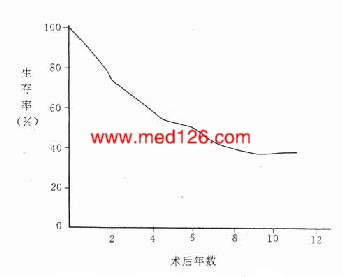
图6-9 607例乳腺癌术后生存率曲线
(医学统计方法,上海科学技术出版社,1978)
预后是用疾病过程中出现某种事件结果的概率来描述。原则上,可通过队列观察,直到所有受观察者都出现该事件结果为止。但是,这种方法失访率高、效率低,故常用寿命表分析法,可较少受到失访的影响。寿命表法应用于死亡和尚存,也就是说这些被观察和随访的病人判定的终点。有时不一定用死亡,而是用某些事前明确规定的症状的出现作为终点。如我们可以观察或随访癌症病人手术后复发率取代死亡率等。因此,寿命表法不仅可用于生命分析,还可用于对其他结局:如肿瘤的复发、排斥或再感染等任何定期随访获得的事件的计数资料指标的分析比较。只要该事件是两分的(即不是……就是)而且在随访期间只发生一次,均能用寿命表法加以研究。
附表1 两组百分比相差显著时所需例数(Ⅰ)
|
甲组 |
乙组百分比 | ||||||||||||||||||||||
| 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 | |||
| 0 | ― | 200 | 100 | 60 | 45 | 36 | 30 | 26 | 23 | 18 | 16 | 15 | 14 | 13 | 10 | 10 | 9 | 9 | 8 | 8 | 6 | ||
| 5 | 200 | ― | 480 | 160 | 95 | 60 | 50 | 38 | 33 | 27 | 20 | 1 | 17 | 16 | 13 | 12 | 12 | 11 | 9 | 9 | 8 | ||
| 10 | 100 | 480 | ― | 720 | 220 | 120 | 77 | 58 | 40 | 36 | 28 | 26 | 20 | 18 | 16 | 15 | 14 | 12 | 9 | 9 | 8 | ||
| 15 | 60 | 160 | 720 | ― | 940 | 272 | 140 | 86 | 60 | 49 | 38 | 32 | 25 | 20 | 19 | 16 | 15 | 12 | 12 | 11 | 9 | ||
| 20 | 45 | 95 | 220 | 940 | ― | 1120 | 310 | 163 | 95 | 65 | 48 | 39 | 30 | 25 | 20 | 19 | 15 | 15 | 14 | 12 | 9 | ||
| 25 | 36 | 60 | 120 | 272 | 1120 | ― | 1280 | 352 | 175 | 100 | 68 | 51 | 40 | 31 | 26 | 20 | 19 | 16 | 15 | 12 | 10 | ||
| 30 | 30 | 50 | 77 | 140 | 310 | 1280 | ― | 1400 | 370 | 180 | 106 | 73 | 50 | 40 | 30 | 26 | 20 | 19 | 16 | 13 | 10 | ||
| 35 | 26 | 38 | 58 | 86 | 163 | 352 | 1400 | ― | 1500 | 400 | 180 | 113 | 74 | 51 | 40 | 31 | 25 | 20 | 18 | 16 | 13 | ||
| 40 | 23 | 33 | 40 | 60 | 95 | 175 | 370 | 1500 | ― | 1560 | 410 | 190 | 114 | 74 | 50 | 40 | 30 | 25 | 20 | 17 | 14 | ||
| 45 | 18 | 27 | 36 | 49 | 65 | 100 | 180 | 400 | 1560 | ― | 1580 | 415 | 190 | 113 | 73 | 51 | 39 | 32 | 26 | 19 | 15 | ||
| 50 | 16 | 20 | 28 | 38 | 48 | 68 | 106 | 180 | 410 | 1580 | ― | 1580 | 410 | 180 | 106 | 68 | 48 | 38 | 28 | 20 | 16 | ||
附表2 两组百分比相差非常显著时所需例数(Ⅱ)
| 甲组百分比 |
乙组百分比 | ||||||||||||||||||||
| 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 | |
| 0 | ― | 300 | 150 | 100 | 70 | 56 | 47 | 38 | 33 | 29 | 24 | 22 | 20 | 17 | 16 | 15 | 14 | 12 | 12 | 11 | 9 |
| 5 | 300 | ― | 780 | 260 | 155 | 100 | 77 | 58 | 40 | 38 | 34 | 30 | 27 | 25 | 19 | 18 | 17 | 15 | 14 | 12 | 11 |
| 10 | 150 | 780 | ― | 1220 | 360 | 188 | 120 | 89 | 68 | 54 | 40 | 37 | 30 | 27 | 25 | 20 | 18 | 17 | 15 | 14 | 12 |
| 15 | 100 | 260 | 220 | ― | 1580 | 460 | 220 | 140 | 98 | 76 | 58 | 46 | 39 | 33 | 26 | 24 | 20 | 18 | 17 | 15 | 12 |
| 20 | 70 | 155 | 360 | 1580 | ― | 1900 | 520 | 255 | 150 | 105 | 78 | 60 | 45 | 39 | 34 | 28 | 24 | 20 | 18 | 17 | 14 |
| 25 | 56 | 100 | 188 | 460 | 1900 | ― | 2180 | 580 | 280 | 168 | 108 | 80 | 60 | 48 | 40 | 35 | 28 | 24 | 20 | 18 | 15 |
| 30 | 47 | 77 | 120 | 220 | 520 | 2180 | ― | 2380 | 630 | 296 | 170 | 119 | 80 | 60 | 50 | 40 | 34 | 26 | 25 | 19 | 16 |
| 35 | 38 | 58 | 89 | 140 | 255 | 580 | 2380 | ― | 2540 | 674 | 308 | 180 | 120 | 85 | 60 | 48 | 39 | 33 | 27 | 25 | 17 |
| 40 | 33 | 48 | 68 | 98 | 150 | 280 | 630 | 2540 | ― | 2660 | 680 | 315 | 180 | 120 | 80 | 60 | 45 | 39 | 30 | 27 | 20 |
| 45 | 29 | 38 | 54 | 76 | 105 | 168 | 296 | 674 | 2660 | ― | 2700 | 693 | 315 | 180 | 119 | 80 | 60 | 46 | 37 | 30 | 22 |
| 50 | 24 | 34 | 40 | 58 | 78 | 108 | 170 | 308 | 680 | 2700 | ― | 2700 | 680 | 308 | 170 | 108 | 78 | 58 | 40 | 34 | 24 |